LUMINANCE CONTRAST

This page discusses the psychophysical concept of luminance contrast and its use in practical applications.

Why Luminance Contrast?

Sensitivity to Change. In designing graphics for usability we are usually not as concerned with the absolute luminances of objects as we are with their luminances relative to the other luminances in the display. The legibility and salience of a symbol, for example, are more strongly influenced by the relationship between its luminance and the luminance of its immediate background than by its own absolute luminance.

Human sensory systems (vision, audition, olfaction, taste, touch, temperature) are organized to respond strongly to temporal and spatial changes in the physical power of the stimulus. When there is a temporal change in the power applied to the sensor (eye, ear, nose, tongue, skin) there is at first a strong response. Then the senses quickly adapt (respond less) to the continued steady application of power.

This high sensitivity to differences is true of vision.

The Concept of Luminance Contrast. Accordingly, we need an engineering concept that characterizes a particular stimulus’s ability to stimulate the differential mechanisms of the visual system. Luminance describes the stimulus power rather than changes of power, so it isn’t enough by itself. The concept of “luminance contrast” was developed for this purpose. Actually we should probably say “concepts”. Several statistics have been proposed for the measurement of luminance contrast. None can be said at this point to have been accepted by the community as universally most useful. All of the luminance contrast statistics would probably be better regarded as practical engineering tools than as descriptions of basic visual function.

Luminance contrast statistics generally have two components:

- The first is the difference between the two luminances in question (e.g., of a symbol and its background). If the state of adaptation of the visual system stays constant, larger luminance differences produce larger brightness differences (higher brightness contrasts).

- The second component of any luminance contrast statistic is some measure describing the adaptation state of the eye. A luminance difference that produces a large brightness difference on a dim background will produce a smaller brightness difference on a brighter background due to visual adaptation. To capture this behavior, designers of luminance contrast statistics generally divide a numerator that describes the luminance change by a denominator that describes the average luminance to which the eye is adapted:

The variety of popular statistics for luminance contrast mostly reflects the fact that the adaptation state of the eye is affected differently by different kinds of stimulus pattern.

The Statistics

Small Symbols on Uniform Backgrounds. The first three measures below can be applied to a common graphic situation, small symbols or text on larger backgrounds of uniform color. For these stimulus patterns the background luminance affects adaptation more than the symbol luminance.

Lightness differences. In graphics that have the appearance of surfaces (like this webpage, for example) it can be useful to describe luminance contrast in terms of the difference between the lightness of the symbol or text and its background, relative to the display's white-point (maximum) luminance. In this website we use a lightness measure called L*.

For a single luminance, L, we define L* as

where Ln is the luminance of the whitepoint, so the difference between the L* of a symbol and the L* of its background is

where Ls, Lb, and Ln are the background, symbol, and white-point luminances, respectively.

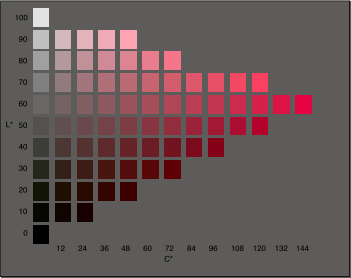
The rows of this chart have the L* values labeled on the left.

If we choose a symbol color from the L* = 30 line and display it on a white background (L* = 100) the lightness difference is delta L* = 70.

This is one expression of the luminance contrast of the symbol on this background.

More about L*

Weber Contrast. One of the oldest luminance contrast statistics, Weber Contrast, is also often used for these patterns (small, sharp-edged graphic objects like symbols and text characters on larger uniform backgrounds):

where Ls is the luminance of the symbol and Lb is the luminance of the immediately adjacent background. Whittle (1994) includes a thorough technical discussion of this type of measure).

When the background is lighter than the symbol CW is negative and ranges from zero to - 1. When the background is darker than the symbol CW is positive and ranges from zero to potentially very large numbers.

Luminance Ratio. Another measure that has often been applied to the same stimulus class is the luminance ratio or its logarithm:

The denominator of CR follows the generic luminance contrast formula in that Lb is often a reasonable estimate of the adapting luminance of the eye for this stimulus class. The numerator, on the other hand, is not the luminance difference between the symbol and background so CR does not behave mathematically like the other contrast measures.

Other Patterns

The above measures are fairly simply applied to the above class of patterns, but there are other classes of pattern for which they are not appropriate.

Michelson Contrast. For simple periodic patterns (e.g., textures) there is no large area of uniform luminance that dominates the user's brightness adaptation. There is no clear choice for the denominator of the above statistics .

Michelson Contrast was developed for this case:

The denominator of CM is twice the mean of the maximum and minimum luminances, i.e., the adaptation luminance estimate is based on the space-average luminance.

Images and Gradients. For contrasts within photos of complicated scenes or on gradient backgrounds the elements of the above statistics are difficult to identify or ambiguous, and they are therefore less useful. More complicated statistics have been proposed for such stimuli (e.g., Peli, 1990). As the use of imagery in information displays increases these more elaborate methods are gaining broader broader usage.  

Comparisons Among Luminance Contrast Statistics

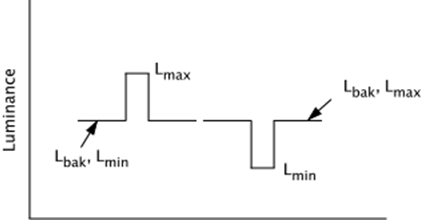
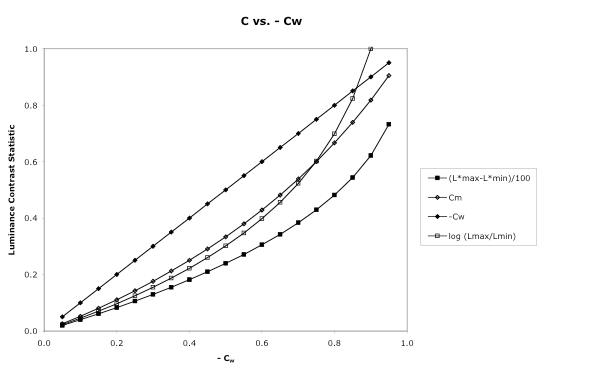
Quantitative comparisons among the various luminance contrast statistics are of limited value because they were designed to describe different spatial patterns and have different mathematical behaviors. Nevertheless in special cases there are a few comparisons that may make them slightly more intelligible. One such case is that noted above, surface-appearance graphics in which the symbols and backgrounds appear to have lightnesses ranging from black to white.

Dark Symbols on Light Backgrounds. Consider a dark line on a white screen, like that diagrammed on the right-hand side of the top figure above. CW and CM can both be unambiguously applied, though CW may provide a more accurate description of brightness differences: its denominator captures that the viewer's brightness adaptation is dominated by the background. Differences of L* should also provide reasonable descriptions of the brightness difference between the line and background. Log CR should also behave reasonably at low contrasts, but will grow rapidly at higher contrasts, where the line's luminance gets small relative to the background's.

We can get a rough idea of the quantitative relationships among the three measures by plotting - CW, CM, log CR, and delta L*/100 as a function of -CW:

In the above comparisons the background was lighter than the symbols. For most work environments the things that the user will be looking at besides the display will have luminances comparable to or lower than the background luminance, so the background luminance is a strong determinant of the adaptation state of the user's visual system. The denominators of L*, CW, CM and log CR are therefore at least rough descriptors of adaptation state for these patterns.

Light Symbols on Dark Backgrounds. When the background is darker than the symbols brightness contrast, acuity, legibility, and other responses may not be as well predicted by the luminance contrast statistics. Aspects of the viewing environment that are not captured by the statistics may strongly affect adaptation and the perceptual responses. The luminance adaptation of a user who is looking back and forth between illuminated papers and a black-background display will be significantly affected by the light coming from the papers. On the other hand, a user whose task involves staring only at the same display in a dark room will be affected mostly by light from the display. Even then, if the symbols are very bright there may still be light scattered within the eye that produces more adaptation than indicated by the luminance of the background alone. Actually, in very bright work environments (e.g., cockpits, Air Traffic Control towers) the same can be true of light background displays. The user's adaptive state may be strongly affected by the bright surroundings, making the statistics less accurate predictors of perceptual performance.

When the background is darker than the symbols the statistics also have more varied mathematical behavior. Those with only the background luminance in the denominator grow very rapidly as the luminance difference increases.

About This Site

Home | Design Process | Color Graphics Topics | Color Tool | Guidelines | Aerospace | Color Science | Utilities

  Site Curator: Richard Mogford | Responsible NASA Official: Richard Mogford | Privacy Statement